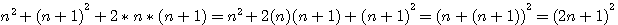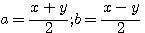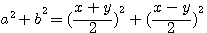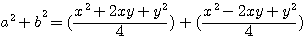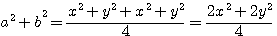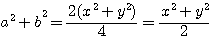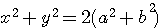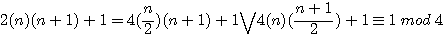Extrapolation à partir d'un carré impair, découpage par n
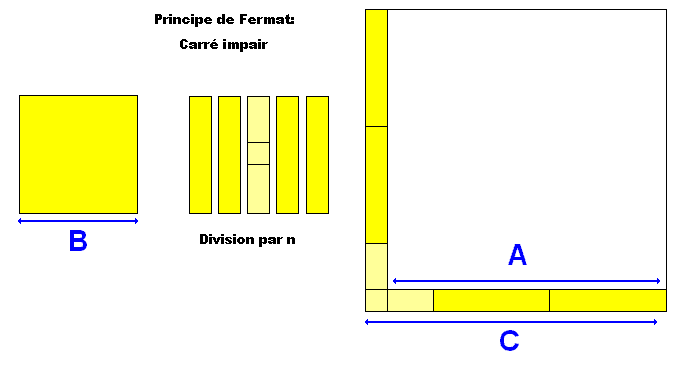
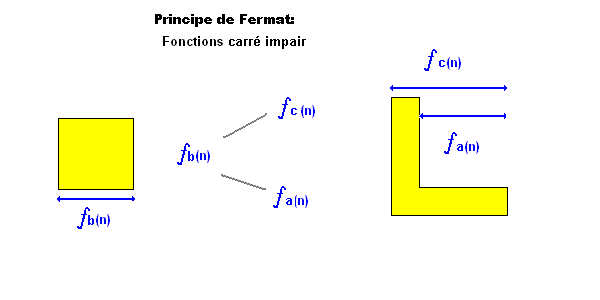
Découpage par n:
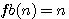
|
Calcul de c (fc(n) |
Calcul de a (fa(n) |
|
factorisation
factorisation
|
factorisation
factorisation
|
verification
C² – A² = B²
(c+a)(c-a)
B²=(fc(n)+fa(n))(fc(n)-fa(n))
B² = ((n²-1)/2 +1 + (n²-1)/2 )((n²-1)/2 +1 - (n²-1)/2 )
B² = ((n²-1)/2 +2/2 + (n²-1)/2 )((n²-1)/2 +2/2 - (n²-1)/2 )
(n²-1)/2 + (n²-1)/2 = 2(n²-1)/2 , Elimination de (n²-1)/2
B² = (2(n²-1)/2 +2/2 )(+2/2 )
B² = (2(n²-1)+2/2 )
B² = (2((n²-1)+1)/2 )
B² = (n²-1)+1
B²=n²
Matrice
| N | C | B (ou A) | A (ou B) | C² | B² | A² | B²+A² |
| 3 | 5 | 4 | 3 | 25 | 16 | 9 | 25 |
| 5 | 13 | 12 | 5 | 169 | 144 | 25 | 169 |
| 7 | 25 | 24 | 7 | 625 | 576 | 49 | 625 |
| 9 | 41 | 40 | 9 | 1681 | 1600 | 81 | 1681 |
| 11 | 61 | 60 | 11 | 3721 | 3600 | 121 | 3721 |
| 13 | 85 | 84 | 13 | 7225 | 7056 | 169 | 7225 |
| 15 | 113 | 112 | 15 | 12769 | 12544 | 225 | 12769 |
| 17 | 145 | 144 | 17 | 21025 | 20736 | 289 | 21025 |
| 19 | 181 | 180 | 19 | 32761 | 32400 | 361 | 32761 |
| 21 | 221 | 220 | 21 | 48841 | 48400 | 441 | 48841 |
| 23 | 265 | 264 | 23 | 70225 | 69696 | 529 | 70225 |
| 25 | 313 | 312 | 25 | 97969 | 97344 | 625 | 97969 |
| 27 | 365 | 364 | 27 | 133225 | 132496 | 729 | 133225 |
| 29 | 421 | 420 | 29 | 177241 | 176400 | 841 | 177241 |
| 31 | 481 | 480 | 31 | 231361 | 230400 | 961 | 231361 |
| 33 | 545 | 544 | 33 | 297025 | 295936 | 1089 | 297025 |
| 35 | 613 | 612 | 35 | 375769 | 374544 | 1225 | 375769 |
| 37 | 685 | 684 | 37 | 469225 | 467856 | 1369 | 469225 |
| 39 | 761 | 760 | 39 | 579121 | 577600 | 1521 | 579121 |
| 41 | 841 | 840 | 41 | 707281 | 705600 | 1681 | 707281 |
| 43 | 925 | 924 | 43 | 855625 | 853776 | 1849 | 855625 |
| 45 | 1013 | 1012 | 45 | 1026169 | 1024144 | 2025 | 1026169 |
| 47 | 1105 | 1104 | 47 | 1221025 | 1218816 | 2209 | 1221025 |
| 49 | 1201 | 1200 | 49 | 1442401 | 1440000 | 2401 | 1442401 |
| 51 | 1301 | 1300 | 51 | 1692601 | 1690000 | 2601 | 1692601 |
| 53 | 1405 | 1404 | 53 | 1974025 | 1971216 | 2809 | 1974025 |
| 55 | 1513 | 1512 | 55 | 2289169 | 2286144 | 3025 | 2289169 |
TOUT carré impair est la double somme de deux carrés : x²=2Z
Introduction:
Dans ce chapitre nous étudions les nombres impairs car 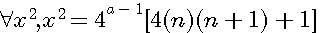 , tout carré pair étant divisible par 4 jusqu'a obtention d'un carré impair de la forme 4(n)(n+1)+1.
, tout carré pair étant divisible par 4 jusqu'a obtention d'un carré impair de la forme 4(n)(n+1)+1.
J'avais (topologie des carrés impairs) expliqué qu'avec tout nombre impair , l'on pouvait trouver l'hypothénuse correspondante pas la fonction 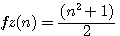 sans toutefois trouver la relation de cette fonction et les travaux de Fermat
sans toutefois trouver la relation de cette fonction et les travaux de Fermat
Multiple de carrés impairs:
Soit x un nombre impair quelquonque ,il est le multiple d'au moins deux nombres impair même si il est premier : par exemple 15 = 3*5 mais aussi 13 (nombre premier) = 13*1. Donc X=X*1
Nous en déduisons donc que tout carré impair et le multiple d'au moins deux carrés impair : 15² = 3² x 5² mais aussi 15² = 15² x 1².Donc :
|
|
exemple : si 15² = 3²5² , 15² est aussi = 15²*1² et donc égal à [14*16+1]*1
Si x est le produit d'au moins deux nombre impair quelconque alors
|
|
15² = 5²*3² =[(4x6)+1]x[(2x4)+1] =(24+1)(8+1)=5²*3²=225 , 21²=7²*3² = [(6x8)+1]x[(2x4)+1]=(48+1)(8+1)
|
Somme des Facteurs x² * 1² :
Si
exemple 15=3*5 est aussi égal à 15*1 , donc 15²+1² = [(15-1)(15+1)+1]+1²=14*16+2 , = 4(7x8)+2
Avec cette équation il est très difficile de prouver qu'elle est égale à 2Z examinons maintenant (2n+1)²....
Somme des facteurs (2n+1)² * 1² :
D'une part : D'autre part : si X est impair alors
Donc
Je ne vous fait pas l'injure de vous rappeler que a²+2ab+b² = (a+b)² |
Soit xy impair alors x²+y² = 2Z
soit X et Y deux nombres impairs alors il exite deux nombres a,b tel que :
Exemple : 21 = 3*7 , a=(7+3)/2=5 , b=(7-3)/2=2
x²+y²=2(a²+b²) :
|
Relation avec 4n+1 premier ou comment Fermat a trouvé ce théorème , premières conclusions:
Si donc le coté d'un carré est premier c'est à dire de forme (2n+1)*1 seulement alors (2n+1)²+1² = 2(n)(n+1)+1 , comme n ou n+1 est divisible par 2 alors :
|
|
Exemple: si x=5 alors 5²+1=26 / 2 = 13 ; si x=5 = (2*2+1) , n=2 ; 2(2)(3)+1 = 13 = 4(2/2)(2+1)+1 =4(1)(3)+1 = 4(3)+1 est donc de type 4n+1
Pour le moment , je prouve que si le coté est premier alors 2Z est de type 4n+1 mais nous n'avons pas encore vu que certains coté non premiers peuvent aussi aboutir à une hypothénuse première :
OBS. DE FERMAT livre V question 12 : Le nombre 21 ne peut pas être divisé en fraction en deux carrés, nous pouvons facilement démontrer cela , et plus généralement, que tout nombre dont le tiers n'est pas lui même divisible par trois, ne peut être décomposé en deux carrés , ni entiers ni fractionnaires.
Par exemple 21 n'est pas une hypothénuse mais le coté du triangle 21²+20²=29²

Patrick Stoltz le 19/02/2009 – dépôt INPI n°: 343319 -
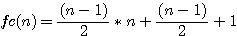
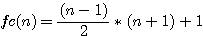
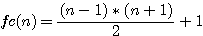
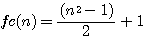
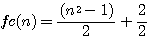
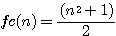
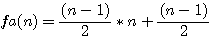
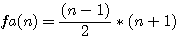
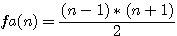
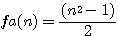
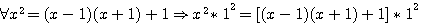
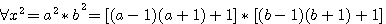
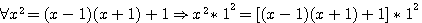 la somme des deux facteurs est égale à :
la somme des deux facteurs est égale à :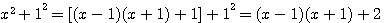
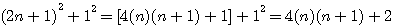
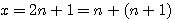 ,
, 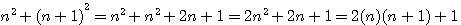
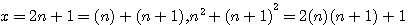
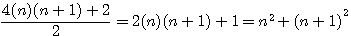
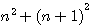 est une hypothénuse :
est une hypothénuse :