|
(not released) |
 |
Ce site est dédié à l'études des mathématiques anciennes et plus particulierement à l'étude de l'arithmetica de Diophante.
Par la suite,cet arithmetica fut etudié et annoté par Bachet (1581-1638) , par Pierre de Fermat(1601-1665) et en 1853 par Emile Brassine.
Grâce à l'analyse détaillée de ces études, j'ai pu simplifier bon nombres de démonstrations d'équations et inventer de nouveaux tutos (pages sur ce site et vidéos you tubes) et poursuivre des recherches suplémentaires (section bonus)
Index des pages Arithmetica / Tutoriels / Bonus
|
|
L'arithmetica de Diophante (environ 200-300) est une liste de questions arithmétiques contenues dans 6 livres . C'est au cours de l'étude du livre II paragraphe 9 que Fermat a posé son grand théorème. Dans cette section sont détaillés bon nombres de question et plus particulièrement les questions annotées par Pierre de Fermat |
|
|
Grâce à cette étude , j'ai élaboré de nouvelles demonstrations de formules mathématiques et théorème que j'ai pu tellement simplifier que j'ai pu réaliser des tutoriels vidéos en les visualisant en quelques lignes d'équations simple (niveau collège) et même avec des morceaux de sucres, cartes à jouer... |
|
|
Dans cette section vous trouverez mes études complémentaires, mes notes additionnelles , et des programmes informatiques créés pour m' aider dans mes recherches. |
Contacter / Presence sur les réseaux sociaux |
|
|
|
Liste des réseaux sociaux où me trouver et formulaire pour me contacter. |
Vidéos youtubes schemath.com
Cliquez sur
Actualités schemath.com sur Tweeter
|
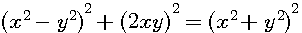
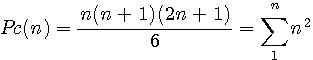
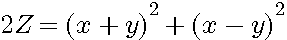
pour afficher la liste des vidéos
