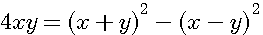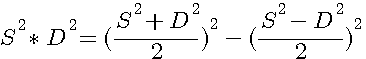Nouveaux Tutoriels

Dans cette section nous abordons de nouveaux théorèmes JAMAIS abordés dans les cours de mathématiques et qui ont permis à Pierre de Fermat d'élaborer de nouveaux théorèmes totalement oubliés aujourd'hui

	Aspect fondamental des nombres (question 30 du livre 1 de l'arithmética) : Soit une somme S de deux nombres x et y et leurs différence D, trouver ces deux nombres S*D = (x+y)(x-y) = S*D + y² = x² et S*D + 2y² = x²+y² Divisibilité de SD par 3 4xy = S² - D² =>
	Soit Z une somme de 2 carrés x²+y² , S=x+y , D= x-y ,  S²+D² = 2Z = 2x²+2y²
	Soit S une somme de 2 nombres au carré (x+y)² D une différence de 2 nombres au carré (x-y)² alors : qui aboutit à L'équation de Diophante:
	Soit un triangle rectangle de coté b & h et d'hypoténuse z , b² + h² = z² => z²=(x²+y²)² b²=(x²-y²)² h² =4x²y²= (2xy)²

Tutos et programmes informatiques schemath.com

Page sur le complément à deux , artifice binaire pour les nombres négatifs

Programmes téléchargeables

eq_simplifier permet de dévelloper / regroupement d'expressions arithmetiques , et montre toutes les étapes : dévellopement , regroupements et calculs +/- de suppressions des parenthèses

Programme pour calculer avec les nombres "modulaires"