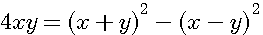|
S*D
|
[ 2(s)+1 ][ 2(d) + 1 ]
|
+ 2(s-d)²
|
=(s+d+1)²+(s-d)²
|
x²+y²
|
|
|
|
7*3
|
[ 2(3)+1 ][ 2(1) + 1 ]
|
+ 2(3-1)²
|
=(3+1+1)²+(3-1)²
|
5²+2²
|
=29
|
4(7)+1
|
|
9*1
|
[ 2(4)+1 ][ 2(0) + 1 ]
|
+ 2(4-0)²
|
=(4+0+1)²+(4-0)²
|
5²+4²
|
=41
|
4(10)+1
|
|
11*5
|
[ 2(5)+1 ][ 2(2) + 1 ]
|
+ 2(5-2)²
|
=(5+2+1)²+(5-2)²
|
8²+3²
|
=73
|
4(18)+1
|
En résumé :
|
si x+y et x-y impair alors (x+y)(x-y)+2y²=Z=x²+y²
Z=[ 2s+1 ]*[ 2d + 1 ]+2(s-d)² =
Z=(s+d+1)²+(s-d)²
et/ou (s-d+2d+1)²+(s-d)² = [(s-d)+D]²+(s-d)²
|
nota:
 [2s+1] = s+(s+1) ; [2d+1] = d+(d+1) [2s+1] = s+(s+1) ; [2d+1] = d+(d+1)
 Soit SD+2y² D<S alors (s-d) négatif devient positif (- (s-d) )² Soit SD+2y² D<S alors (s-d) négatif devient positif (- (s-d) )²
 Soit SD+2y² => (s-d)² = (d-s)² Soit SD+2y² => (s-d)² = (d-s)²
 Si S=D alors => s=n , d=n => [2(n)+1][2(n)+1]+0² = (2n+1)² Si S=D alors => s=n , d=n => [2(n)+1][2(n)+1]+0² = (2n+1)²
 Si S et D = 0 alors 1*1 = 1² + 0² Si S et D = 0 alors 1*1 = 1² + 0²
 Si D=1 , d=0 alors [ 2(s)+1 ][ 2(d) + 1 ]+2(s-d)² devient [ 2(s)+1 ]*1+2(s)² = (s+1)²+s² Si D=1 , d=0 alors [ 2(s)+1 ][ 2(d) + 1 ]+2(s-d)² devient [ 2(s)+1 ]*1+2(s)² = (s+1)²+s²
Exemples : 11*1 + (s)² = [2(5)+1]*1+2*5² =11 + 50 = (5+1)² + 5² = 6²+5² = 61
7*1 = [2(3)+1]*1 +2*3² =7+18 = (3+1)²+3² = 4²+3² = 25 .... = 5² ....
 Z= (s-d + 2d+1)² + (s-d)² = (s-d + D)² + (s-d)² Z= (s-d + 2d+1)² + (s-d)² = (s-d + D)² + (s-d)²
A ce stade il est TRES IMPORTANT de noter que pour TOUT S*D nous ne produisont PAS des 4n+1 premiers à tous les coups (si par exemple S ou D non premier...)
Pourquoi ce système ?
Celà peut paraître tiré par les cheveux et une complexité inutile et pourtant :
|
X*Y
|
=X*Y
|
6*7=42
|
|
S=(x+y) D=(x-y)
le 2éme facteur est plus petit que le premier
|
SD=(x+y)(x-y)=x²-y²
|
7*6 x=13/2 y=1/2 S=(13/2+1/2)(13/2-1/2)
(13/2)²-(1/2)²
|
|
S=(x+y) impair D=(x-y) impair
|
SD=(2s+1)(2d+1)
x=(2s+2d+2)/2 = s+d+1
y=(2s-2d)/2 = s-d
|
7*3=[2(3)+1][2(1)+1]
x=3+1+1=5 y =3-1=2
7*3=(5+2)(5-2)=5²-2²
|
Déjà nous pouvons voir plusieurs avantages :
 Cela permet de poser des équations en évitant de dire à chaque fois si S et D impair et de poser des équations sans fractions , en effet si S ou D , S=(x+y); D=(x-y) est pair alors je dois écrire x=(S+D)/2 ; y = (S-D)/2 , par exemple S=10 D=3 => x=13/2 y=7/2 , S= (13/2+7/2)=20/2=10 ..... Cela permet de poser des équations en évitant de dire à chaque fois si S et D impair et de poser des équations sans fractions , en effet si S ou D , S=(x+y); D=(x-y) est pair alors je dois écrire x=(S+D)/2 ; y = (S-D)/2 , par exemple S=10 D=3 => x=13/2 y=7/2 , S= (13/2+7/2)=20/2=10 .....
 Soit Z = X² + Y² cela permet de quantifier x²+y² = (s+d+1)² + (s-d)² Soit Z = X² + Y² cela permet de quantifier x²+y² = (s+d+1)² + (s-d)²
 Puisque s+d+1 est aussi égal à s-d+2d+1 celà permet de noter x²-y² : Puisque s+d+1 est aussi égal à s-d+2d+1 celà permet de noter x²-y² :
(s+d+1)² - (s-d)² = (s-d+2d+1)² - (s-d)² =>si n=s-d alors x²-y² = (n+2d+1)²-n² > x²+y² = (n+2d+1)²+n²
 Permet de différencier 1 d'une factorisation et 1 une unité , et aussi 1 de 1² Permet de différencier 1 d'une factorisation et 1 une unité , et aussi 1 de 1²
par exemple n²+n = n(n+1) , 1 est issu d'une factorisation ; si Z = 4²+1² quelle est la valeur de 1² ? un nombre de la forme 4n+1 est t'il 4n+1 ou 4n+1² ....
si 4n+1 est premier alors Z = x²+y²
Nous formons des hypoténuses de la forme 4n+1 mais nous ne prouvons pas que cette hypoténuse formée est première , nous cherchons maintenant l'inverse
Livre III question 22 (L3Q22) :
OBS DE FERMAT. Un nombre premier qui surpasse de 1 tout multiple de 4 , est une seule fois l'hypoténuse d'un triangle rectangle (formé de coté entiers), son carré deux fois, son cube trois fois , sa quatrième puissance quatre fois, etc à l'infini.
Nous pouvons en déduire que :
Nous avons formé ces hypoténuses à partir de SD produit de 2 nombres impair *1 (donc D et D premier ) et non pas 3 nombres impairs
Avec 3 nombres impairs nous aurions SD=abc*1 = (ab)c*1 ou a(bc)*1 si je nomme le troisième facteur k impair nous avons kSD ou SkD donc
|
2Z = (kS)² + D² ou S² + (kD)²
|
Pour que 2Z soit la somme de 2 carrés il faut k²(S²+D²) et non pas k(S²+D²)
Si 1*premier = 4(n) + 1 alors 2Z = 2*premier = 8n + 2 ; 2Z - 2 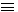 n (mod 8) n (mod 8)
Si k pair 2*premier n'est plus premier parce que divisible par 2
Donc cela suppose qu'a partir d'un double premier de forme 8n+2 nous pouvons former un double carré impair.
|

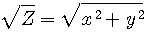
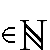
 ou
ou