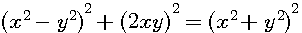Ce que Fermat m'a appris de fondamental c'est qu'il ne faut pas étudier A²+B² = C² mais, est t'il possible de séparer C² en 2 autres carrés ... ?

Tout savoir sur ce qu'est une hypoténuse...

Comprendre le Théorème de Pythagore

Vous avez tous appris le fameux théorème de Pythagore applicable au triangle rectangle : x²+y²=z² (ou a²+b²=c²) ou sous la forme :

(coté du carré z)

Précisons et détaillons:

Soit le triangle rectangle du Schema n°1 composé de:

Un coté x ,adjacent de l'angle droit (sur le croquis n°1 c'est la hauteur du triangle rouge)

Un coté y ,l'autre coté adjacent de l'angle droit (la base du triangle rouge)

Un coté z opposé de l'angle droit.

Schema n°2

Pour connaître la longueur du coté de z²:

L'on forme une surface ,un carré, dont le coté est égal à la longueur x . Cette surface aura pour aire (surface) x*x = x²

L'on forme un deuxième carré y², dont le coté est égal à la longueur y

On ajoute ces DEUX surfaces pour former UNE nouvelle surface DE FORME carrée, appelée carré de hypoténuse = z²

On mesure le coté de ce carré z² en appliquant la racine carrée de ce carré z² : = z

Ce coté z est appelé coté de l'hypoténuse

Schema n°1:

Triangle rectangle de cotés :

x et y adjacents à l'angle droit

z opposé à l'angle droit

Schema THEORIQUE n°2:

pythagore

Soit le triangle dit rectangle ayant pour coté de l'angle droit : x et y alors le coté opposé de l'angle droit mesure :

Z²=X²+Y² , son coté z appartient N ou

Exemple 1: 5²+12²=25 +144 =169 (=13²) :

Exemple 2:

Dans ces cas le coté du carré Z² est un entier ou une fraction , ce triangle est "dit RECTANGLE"

PAR CONTRE:

Si je forme un triangle rectangle ayant pour coté 10 et 3 (détaillé au chapitre suivant) alors

(10.44030651*10.44030651 = 109.xxx)

Dans ce cas le coté du carré Z est un réel (nombre à décimales infinies) , ce triangle est dit "QUELCONQUE" parce que non mesurable

Z=x²+y² son coté =

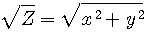
coté hypotenuse n'appartient pas N

par réciproque de Pythagore , si je mesure Z=10 et un coté 3 l'autre coté ne sera pas un nombre entier ou fractionnaire , ce triangle ne sera pas rectangle dans le monde des nombres entiers ou fractionnaires:

10²-3²= 100-9 = 91 ,

Notez que les nombres réels n'existaient pas à l'époque de Fermat , Diophante ou Pythagore

Schema n°3

Z est un carré dont le coté est:

Soit un entier ou une fraction

Soit un réel...

Représentation visuelle d'un carré d'un triangle dit quelconque (Z=x²+y²)

On peut donc penser que l'on ne pourrait pas dessiner un triangle dit "non rectangle" et pourtant Il est parfaitement possible de former un carré Z selon le schéma numéro 3 à partir de importe quelle somme de deux carrés quelconque :

Schema n°4

Du point de vue de la surface d'un triangle , TOUT triangle peut être représenté par un triangle rectangle

Dans TOUS les cas cette surface sera égale à (Base * Hauteur) /2

Nommons:

Hauteur² = y² ; Base² = x²

Du point de vue uniquement de la surface de ce triangle il apparaît comme étant rectangle !!!

Formons un carré Z : Mesurons un carré de coté x-y et on le retire du plus grand des deux carrés

Schema n°5

Schema n°6:

le carré jaune = (x-y)²

nota : si y > x alors (négatif)² => positif

Nous obtenons 2 rectangles (en rouge) de coté x*y et donc quatre triangle rectangles

Surface d'un triangle = xy/2

, 4 triangles rouges = 4xy/2 = 2xy

donc :

x²+y² = (x-y)² + 2xy

Exemples:

2²+5² =29= (5-2)²+2*2*5 = 9+20

3²+5²=34= (3-5)²+2*3*5 = 4+30

3²+ 4²=5²=25 = (1)²+2*3*4=1+2

Nous pouvons former maintenant Z à partir des 4 triangles rouges et le carré (x-y)

Nota: Le coté du carré vert (x-y)² n'est pas parallèle au coté Z

formule de toutes hypoténuses

En résumé :

Z=2xy+(x-y)²=x²+y²

(2xy+x²-2xy+y²=x²+y²)

Z=-2xy+(x+y)²=x²+y²

(-2xy+x²+2xy+y²=x²+y²)

Il est intéressant aussi de noter que TOUTES difference de 2 nombres au carré + 8 triangles rectangle rouges , (x-y)²+8*(xy/2) , forment toujours un carré (égal à (x+y)²)

(x-y)²+4xy=(x+y)²

voir arithmetica livre 1 Question 30

Z = x²+y² donc Z² = (x²+y²)² et non pas x²+y²

A l'époque où a été utilisée l'hypoténuse, les nombres reels , les mots "racines carrées" , n'existaient pas.

En effet, les anciens n'étudiaient pas la longueur en tant que telle mais les surfaces et les rapports (fractions) ainsi formés.

Diophante et Fermat, ne connaissant pas les nombres réels , ils examinèrent donc les 3 surfaces formées par un triangle rectangles représentées sur le Schema n°3:

X²,Y², Z , et aussi le triangle rouge de surface = xy/2

Ils considèrent donc qu'une hypoténuse est la somme de 2 carrés quelconque Z=x²+y²; ( rappel , son coté est un reel ) et donc qu'une hypoténuse carrée et la somme carrée de ces deux carrés quelconques Z²=(x²+y²)² qui est donc différent de x²+y²

Exemple 2²+3² = 13 ; (2²+3²)² + 0 = 13² , par contre l'on peut separer 13² en deux autres carrés (5²+12²) mais tous les carrés ne sont pas divisibles en 2 autres carrés ... (c'est une grande partie des théories de Fermat)